Explainability in Neural Networks, Part 3: The Axioms of Attribution

Unlike predictive models, for attribution methods there is no universal measure of "accuracy" or "correctness"; we can only say whether a method is intuitively "reasonable" or not, and we saw some examples of this analysis in the previous post. It is therefore common in this area to take an axiomatic approach: formalize certain "desirable" properties of attribution methods as Axioms, to help guide the design and evaluation of attribution methods. This post will describe a set of such axioms, based on the ICML 2017 paper of Sundararajan et al ^[1] (which is an excellent read on the subject).

Recall that we denote the function computed by the neural network as $F(x)$, where $x$ is the $d$-dimensional input vector. If $b$ is the baseline input vector, the attribution of the difference $F(x) - F(b)$ to feature $x_i$ is denoted by $A^F_i(x; b)$. To avoid notational clutter in this post we will assume that $b$ is the all-zeros vector, and that $F(b) = 0$, and we will simply write $A^F_i(x)$ to denote the attribution of $F(x)$ to feature $x_i$. As a running example we will continue to use the function $F(x) = \min(1, x_1 + x_2)$.

Axiom: Completeness

We mentioned this axiom in the last two posts:

Completeness: For any input $x$, the sum of the feature attributions equals $F(x)$:

\begin{equation*} F(x) = \sum_i A_i^F(x) \end{equation*}

Why is this property called "completeness"? Because any attribution method satisfying this axiom "completely" accounts for the value of $F(x)$ in terms of the feature attributions.

We saw in the last post that the perturbation method fails to satisfy completeness: If $F(x) = \min(1, x_1 + x_2)$, then for $x = (2,2)$, $F(x) = 1$, but $F((0,2)) = F((2,0)) = 1$, meaning that perturbing either input individually to 0 does not alter the function value, and this method would attribute 0 to both features, clearly violating Completeness.

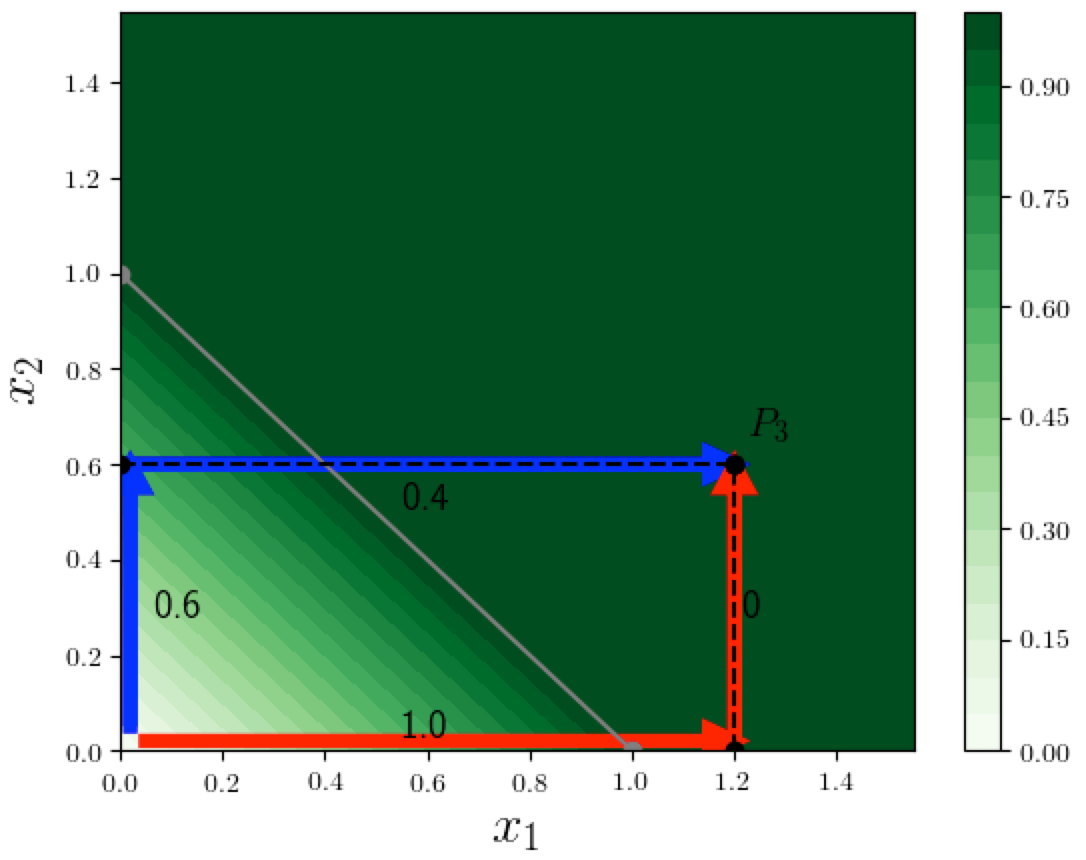
On the other hand we saw in the last post that a certain path method does satisfy Completeness. Recall that the path method consists of picking a path from the origin (zero vector) to $x$, and computing how much each feature contributes along this path. In the figure below, to calculate the attributions at $P_3 = (1.2, 0.6)$, we considered two paths from the origin to $P_3$. Each segment of the path sequentially varies a single feature, keeping the other features (just one in this 2D case) constant. For example if we choose to do attribution using the blue path from the origin to $P_3$, then on the first segment only $x_2$ changes (from 0 to its final value 0.6), and causes $F$ to increase by $0.6$, and on the second segment only $x_1$ changes, and causes $F$ to increase by $0.4$, which results in attributions $(0.4, 0.6)$, which sum to 1. Similarly, the red path yields attributions $(1,0)$, which again sum to 1.

Axiom: Sensitivity

There are two versions of this axiom:

Sensitivity: If $x$ has only one non-zero feature and $F(x) \neq 0$, then the attribution to that feature should be non-zero.

Insensitivity: If $F(x)$ does not mathematically depend on the value of a feature $x_i$ then the attribution to $x_i$ should always be zero.

It is easily verified that: (a) Perturbation methods satisfy Sensitivity, and (b) Completeness implies Sensitivity, so the Path method satisfies this axiom as well. However another method we saw in the last post, the gradient method, does not. In our example, at the point $x = (2,0)$, $F(x)=1$ but the gradient of $F(x)$ with respect to $x_1$ is 0, which would be the gradient-based attribution. The reason the gradient method violates Sensitivity is that gradients are local. All methods we've seen so far satisfy the Insensitivity axiom.

Axiom: Implementation Invariance

Implementation Invariance: When two neural networks compute the same mathematical function $F(x)$, regardless of how differently they are implemented, the attributions to all features should always be identical.

This one might seem completely un-controversial, but surprisingly enough there are some attribution methods that violate this (e.g. DeepLift^[2] and Layer-wise Relevance Propagation or LRP^[3]). All the methods we have seen, however, do satisfy this axiom, since none of them refer to the implementation details of $F(x)$.

Axiom: Linearity

Linearity: If we linearly compose two neural networks computing $F$ and $G$ to form a new neural network that computes $H = aF + bG$, then for any feature $x_i$, its attribution for $H$ is a weighted sum of the attributions for $F$ and $G$, with weights $a$ and $b$ respectively, i.e.,

\begin{equation*} A_i^{H}(x) = a A_i^F(x) + b A_i^G(x) \end{equation*}

In other words, this axiom says that the attribution method should preserve linearity.

Axiom: Symmetry-Preserving

Two features are said to be symmetric with respect to a function $F(x)$ if interchanging them does not change the function mathematically. For example $x_1, x_2$ are symmetric in $F(x) = \min(1, x_1 + x_2)$, but they are not symmetric in $F(x) = 3x_1 + x_2$. The following axiom states that an attribution method must preserve symmetry:

Symmetry-Preserving: For any input $x$ where the values of two symmetric features are the same, their attributions should be identical as well.

Path Methods and Aumann-Shapley Cost-Sharing

We saw a specific path method above: the path starts at the origin, and changes each feature sequentially until the specific input $x$ is reached.
For each segment where a feature $x_i$ is changed (and all others are kept constant), we then calculated how much $x_i$ contributed to the change in function value along. The specific paths we considered are axis-parallel paths (since each segment is parallel to some feature-axis), but there is no reason we should restrict ourselves to such paths. On a more general path from the origin to $x$, there is a way to compute the contribution of each variable, using a method called Path Integrated Gradients.

Path Integrated Gradients have an intriguing connection to work by two Nobel-prize winning economists Lloyd Shapley and Robert Aumann on cost-sharing: $F(x)$ represents a project's cost and the "features" are the demands of the participants, and attribution corresponds to cost-shares (or cost-allocations). Specifically,

Attribution based on a Path Integrated Gradient (along any fixed path from the origin to $x$) corresponds to a cost-sharing method referred to as Aumann-Shapley^[4], and it has been proved^[5] that this method is the only one that satisfies all of the above axioms except the Symmetry-Preserving Axiom.

And the paper by Sundararajan et. al.^[1:1] (on which this post is based) proposes a special case of the Path Integrated Gradient and shows:

Attribution using the Integrated Gradient along the straight line from the origin to $x$, is the unique Path Method that is Symmetry-Preserving.

A future post will take a closer look at Path Integrated Gradients.