Can an AI model anticipate how well it will perform in the wild?

In many important applications, AI models are trained on labeled data but when deployed in the wild, labels are not readily available (for example in medical imaging where the model is identifying a cancerous patch, "ground-truth" labels may require expert examination). A critical question is -- in the absence of "ground-truth" labels, how much can we trust the predictions of the model? This blog post describes an intriguing new technique based on training an ensemble of "check" models (on the original labeled training data and the unlabeled test data) in such a way that the correctness of the main model is related to agreement with the check models. This leads to an elegant way to estimate the accuracy of the model on unlabeled data. The full paper^[1] will appear in NeurIPS 2021.

Motivation

When a machine learning model is deployed in the wild, it can encounter test data drawn from distributions different from the training data distribution and suffer a drop in performance. For example, the deep models trained on ImageNet will have large performance drop on the test data from ObjectNet^[2].

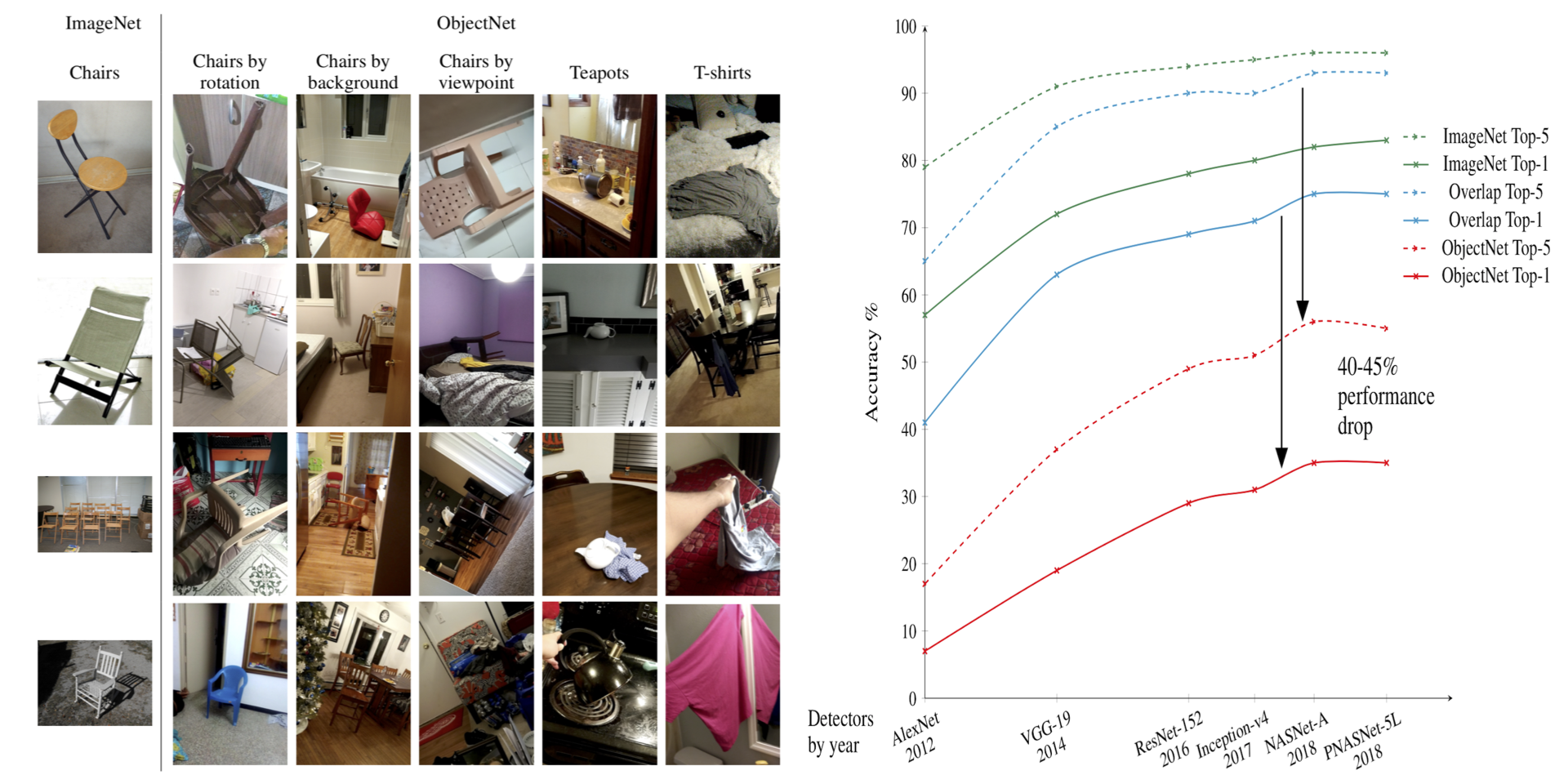
For safe deployment, it is essential to estimate the accuracy of the pre-trained model on the test data. If we have the labels for the test data, then we can simply compute the accuracy of the model. However, the labels for the test inputs are usually not immediately available in practice, and obtaining them can be expensive. This observation leads to a challenging task of unsupervised accuracy estimation -- estimating the accuracy of a pre-trained classifier on a set of unlabeled test inputs. Furthermore, it is beneficial to estimate the correctness of the predictions on individual points. This leads to an even more difficult task of error detection, which aims to identify points in the unlabeled test set that are misclassified by the pre-trained model. Such a finer-grained estimation can facilitate a further improvement of the pre-trained model (e.g., manually label those misclassified data points and retrain the model on them).

Previous Work

While there have been previous attempts to address unsupervised accuracy estimation or the broader problem of error detection, their successes usually rely on some assumptions that may not hold in practice. For example, a natural approach is to use metrics based on model confidence (i.e. softmax probability) to measure the performance of the pre-trained model, e.g., as in ^[3]. If the model is well-calibrated with respect to test data, then the average confidence on the test data approximates its accuracy quite well. However, it has been observed that many machine learning systems, in particular modern neural networks, are poorly calibrated, especially on test data with distribution shifts ^[4][5]. Another method is to learn a regression function that takes statistics about the model and the test data as input and predicts the performance on the test data ^[3:1][6]. This requires training on labeled data from various data distributions, which is very expensive or even impractical. Furthermore, the performance predictor trained on the labeled data may not generalize to unknown data distributions. Recent work by ^[7] proposes to learn a “check” model using domain-invariant representation and use it as a proxy for the unknown true test labels to estimate the performance via error detection. It relies on the success of the domain-invariant representation methods to obtain a highly accurate check model on the test data. Hence, the check model performance suffers when domain-invariant representation is not accurate in circumstances such as test data having outlier feature vectors or different class probabilities than the training data.

Self-training Ensembles: A Quick Tour

Our basic idea is to learn a “check model” $h$ and use the disagreement between $h$ and the pre-trained model $f$ for the tasks of accuracy estimation and error detection: identify a point $x$ as misclassified only if $h$ disagrees with $f$ on $x$.

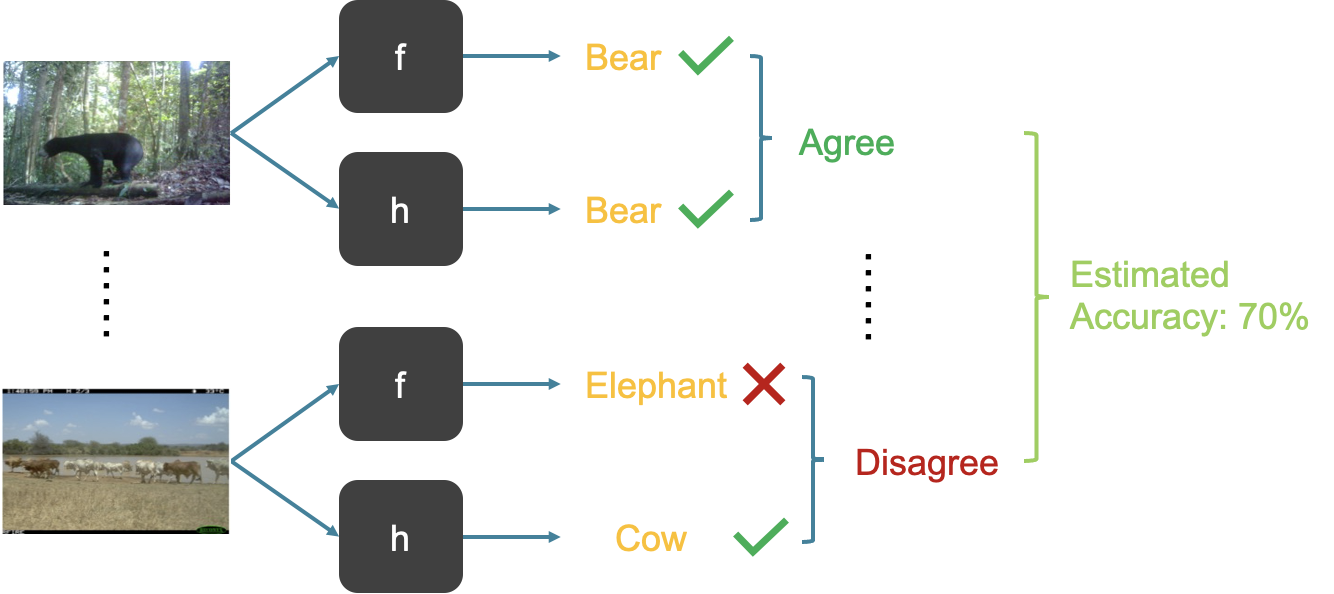
It is easy to understand that the disagreement approach succeeds if: (C1) $h$ agrees with $f$ on points where $f$ is correct; and (C2) $h$ disagrees with $f$ on points where $f$ is incorrect. Our first key observation is that usually (C1) can be satisfied approximately in practice. Intuitively, if we train $h$ and $f$ using the same training data, then $h$ can be trained to be correct on the subset of the instance space where $f$ is correct. However, (C2) is a more tricky condition: when $f$ is incorrect, we would like $h$ to disagree with $f$, which means $h$ can either be correct or make a different mistake than $f$. Thus the condition (C2) may not be easily satisfied since $h$ can make similar mistakes as $f$, which then leads to an overestimation of the accuracy.

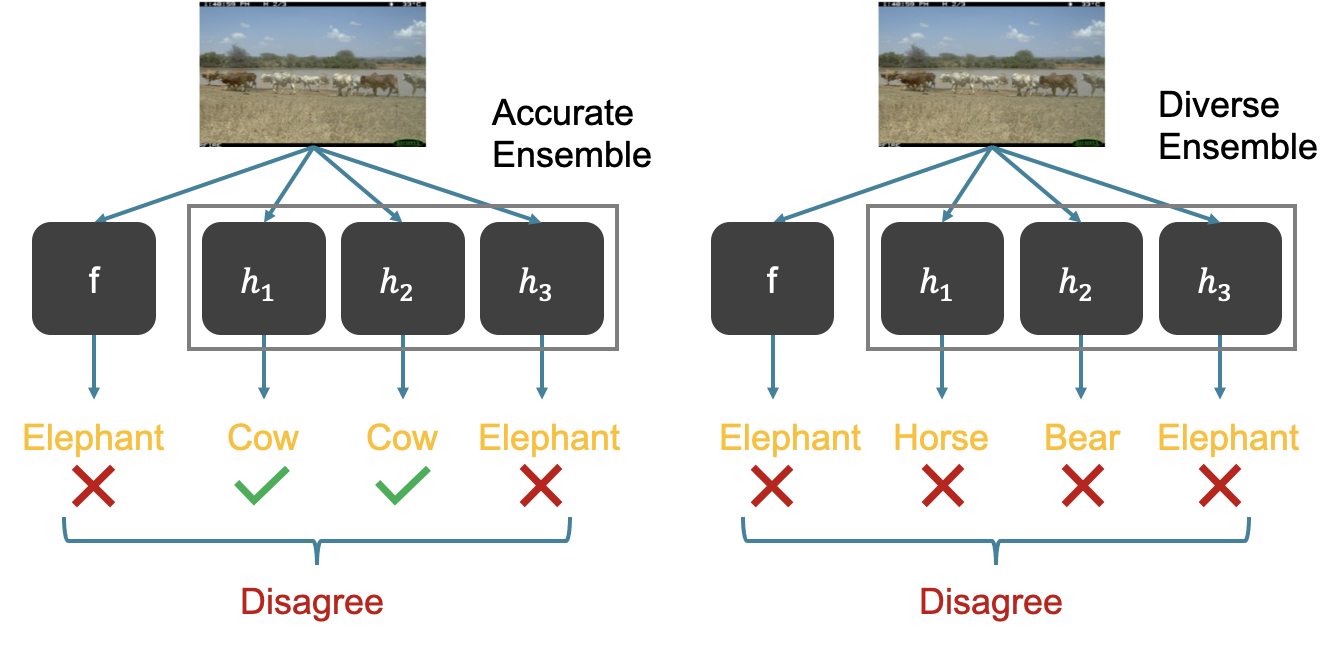
Our focus is to improve the disagreement on misclassified points and we use ensemble and self-training to achieve this. We propose to learn an ensemble of models (instead of one check model) and identify a point $x$ as mis-classified if the ensemble disagrees with $f$ on $x$ (i.e. a large fraction of the models in the ensemble disagree with $f$ on their predictions on $x$). To make the ensemble disagree with $f$ on a mis-classified test input $x$, we have two ways: one is to train accurate models in the ensemble such that they can predict correctly on the test point $x$. The other is to train a diverse ensemble such that they won’t make similar mistakes as $f$. The first way may be achievable when the training data contains information for prediction on $x$. A prototypical example is when the test inputs are corruption of clean data from the training distribution (e.g., the training data are images in sunny days while the test inputs are ones in rainy days), and techniques like unsupervised domain adaptation can be used to improve the prediction on such test inputs. However, correct predictions on $x$ may not be feasible in many interesting scenarios due to insufficient information (e.g., the test image in the open world can contain an object that is never seen in the training data). Fortunately, it has been shown that for such inputs, one can obtain an ensemble of models with diverse predictions (e.g.,^[8]). This then gives the second way to achieve disagreement: using diverse ensembles.

Empirically, we observe that the ensemble may only be able to identify a subset of the mis-classified points. Therefore, we propose to iteratively identify more and more mis-classified points by self-training. For each mis-classified data point $x$ identified by the ensemble, we assign it a pseudo-label that is different from $f(x)$ (e.g. use the majority vote of the ensemble or a random label as the pseudo-label). Then we can train (with regularization) a new ensemble to encourage their disagreement with $f$ on the pseudo-labeled data $R$ (e.g., use a supervised loss on $R$ with a small weight as the regularization).

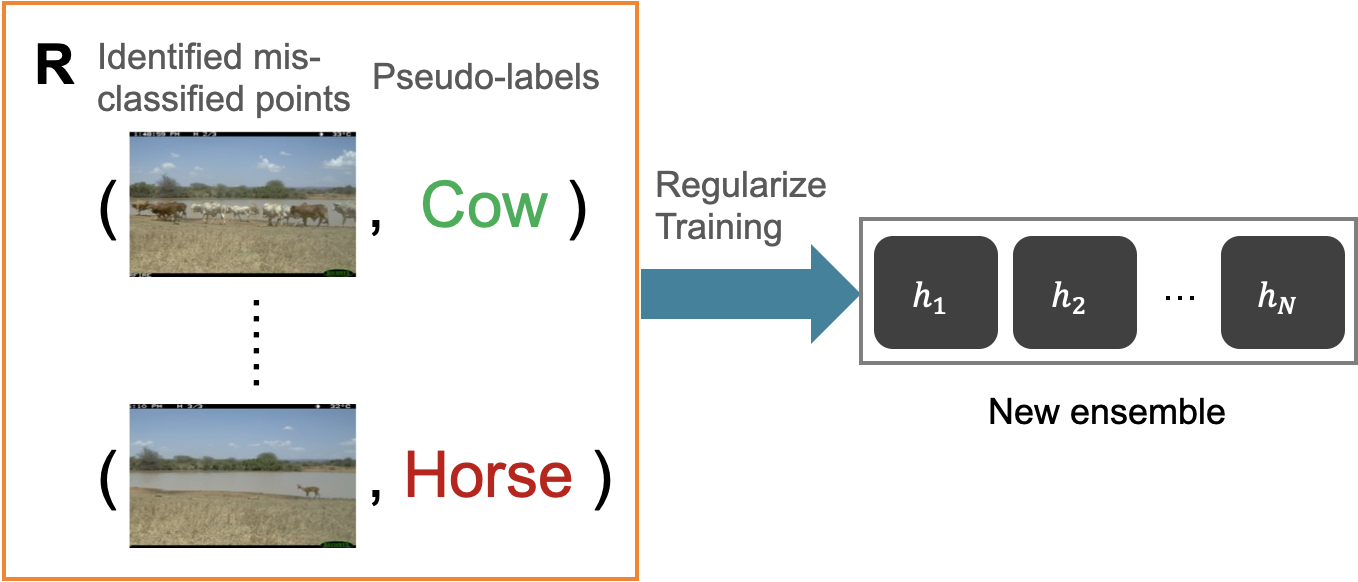
Based on these intuitions, We propose a principled and practically effective framework that makes a novel use of the self-training technique on ensembles for the challenging tasks of accuracy estimation and error detection.

Theoretically, we show that our framework succeeds if in each iteration, the ensemble learned satisfy the following conditions: (A) correct on points where $f$ is correct; (B) mostly disagree with $f$ on the pseudo-labeled data $R_X$; (C) either correct or diverse on $W_X \setminus R_X$, where $W_X$ is the set of misclassified points.

Based on the success conditions of our framework, we propose two concrete ensemble learning methods $\mathcal{T}_{RI}$ and $\mathcal{T}_{RM}$. $\mathcal{T}_{RI}$ trains ensemble models with different random initializations similar to Deep Ensemble^[8:1]. It has been shown that deep models trained from different random initialization can be diverse on outlier data points^[9] and thus can satisfy our condition (C). $\mathcal{T}_{RM}$ trains ensemble models using the representation matching technique (a common approach to improve target accuracy in the domain adaptation problem). We use the checkpoint models during training as the ensemble since we observe that they can have diversity on misclassified data points empirically. Thus, for $\mathcal{T}_{RM}$, our condition (C) can be satisfied better.

We perform experiments for unsupervised accuracy estimation and error detection tasks on 59 pairs of training-test datasets from five dataset categories, including image classification and sentiment classification datasets. In summary, our findings are: (1) Our method achieves state-of-the-art results on both accuracy estimation and error detection tasks. (2) Both ensemble and self-training techniques have positive effects on the tasks and it is easy to pick suitable hyperparameters for our algorithms. (3) Empirical results show that the assumptions made in our analysis hold approximately.

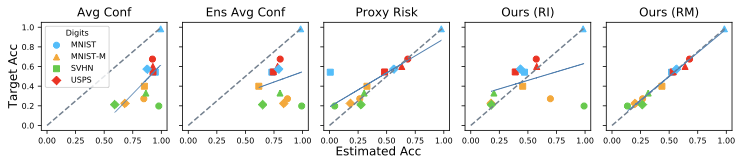
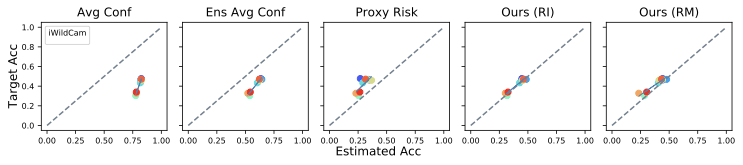
Conclusion

In this blogpost, we present a generic algorithmic framework for the important and challenging tasks of unsupervised accuracy estimation and error detection. The instantiations of our framework show strong empirical results on various datasets for both tasks. It will be of significant interest to extend our methodology to other data modalities such as tabular data and event sequence data. Also, the current methodology applies to models whose output is a class label, and the metric of interest is accuracy. However, there are important settings where the output is a class probability. One very common example of such a setting is probabilistic binary classification, where the model outputs a probability of the “positive” class, and the metric of interest is usually the ROC-AUC or PR-AUC. We plan to extend some of our ideas to this case.